what is the correct code to perform matrix multiplication on the matrix a and b

Overview of Matrix Multiplication in NumPy

Matrix Multiplication in NumPy is a python library used for scientific computing. Using this library, nosotros can perform circuitous matrix operations like multiplication, dot product, multiplicative inverse, etc. in a unmarried stride. In this postal service, nosotros volition exist learning about unlike types of matrix multiplication in the numpy library.

Different Types of Matrix Multiplication

In that location are primarily iii different types of matrix multiplication :

Function	Description
np.matmul(array a, array b)	Returns matrix product of ii given arrays
np.multiply(array a, array b)	Returns chemical element-wise multiplication of two given arrays
np.dot(array a, array b)	Returns scalar or dot production of two given arrays

1. Matrix product of two given arrays

In club to find the matrix production of two given arrays, we can use the following role :

np.matmul(assortment a, array b)

Input for this function cannot be a scalar value

A =	all	a12	a13
	a21	a22	a23

B =	b11	b12	b13
	b21	b22	b23
	b31	b32	b33

A @B =

a11*b11 + a12*b21 + a13*b31	a11*b12 + a12*b22 + a13*b32	a11*b13 + a12*b23 + a13*b33
a21*b11 + a22*b21 + a23*b31	a21*b12 + a22*b22 + a23*b32	a21*b13 + a22*b23 + a23*b33

Example #1

Plan to illustrate the matrix product of two given due north-d arrays.

Code:

import numpy equally np
A = np.array([[1,2,3], [four,v,six]])
B = np.array([[i,1,1], [0,1,0], [one,i,1]])
impress("Matrix A is:\n",A)
print("Matrix A is:\due north",B)
C = np.matmul(A,B)
print("Matrix multiplication of matrix A and B is:\n",C)

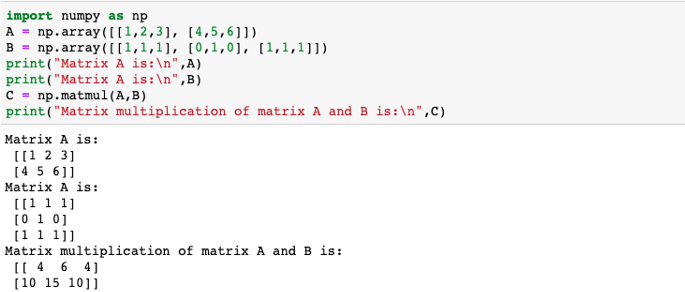
The matrix product of the given arrays is calculated in the following ways:

B=	i	i	1
	0	1	0
	i	i	i

A @ B =

1*1 + two*0 + 3*1 = four	1*i + 2*1 + 3*i = 6	one*1 + two*0 + 3*1 = 4
four*ane + v*0 + half-dozen*1 = 10	4*1 + v*1 + 6*1 = 15	iv*one + v*0 + six*ane = 10

two. Element wise multiplication of two given arrays

In society to find the element-wise production of two given arrays, we can apply the following function.

np.multiply(array a, assortment b)

A =	all	a12	a13
	a21	a22	a23

B =	a21	a22	a23
	a21	a22	a23

A*B =

a11*b11	a12*b12	a13*b13
a21*b21	a22*b22	a23*b23

Instance #2

Plan to illustrate element-wise multiplication of ii given matrices

Code:

import numpy as np
A = np.array([[1,2,iii], [iv,5,six]])
B = np.assortment([[i,2,3], [four,5,6]])
print("Matrix A is:\n",A)
impress("Matrix A is:\due north",B)
C = np.multiply(A,B)
impress("Matrix multiplication of matrix A and B is:\n",C)

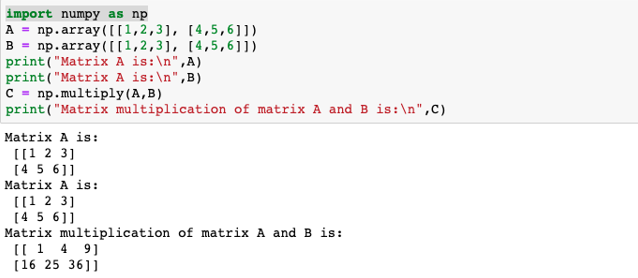
The element-wise matrix multiplication of the given arrays is calculated in the post-obit ways:

B =	1	i	1
	0	1	0
	i	i	1

A * B =

i*1 = 1	2*2 = 4	three*iii = 9
4*iv = 16	five*5 = 25	6*6 = 36

3. Scalar or Dot product of two given arrays

The dot product of whatever two given matrices is basically their matrix product. The just deviation is that in dot production we can take scalar values as well.

A.B = a11*b11 + a12*b12 + a13*b13

Example #3

A program to illustrate dot product of ii given ane-D matrices

Code:

import numpy as np
A = np.array([1,2,iii])
B = np.array([4,5,half-dozen])
print("Matrix A is:\due north",A)
print("Matrix A is:\n",B)
C = np.dot(A,B)
impress("Matrix multiplication of matrix A and B is:\n",C)

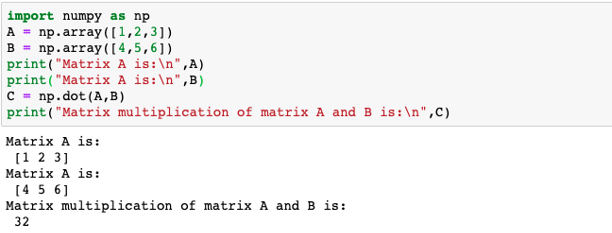
The dot production of two given 1-D arrays is calculated in the post-obit ways:

A.B = 1*4 + two*v + 3*half dozen = 32

Case #4

A program to illustrate dot product of ii given ii-D matrices

Code:

import numpy equally np
A = np.array([[one,2],[2,1]])
B = np.assortment([[4,5],[4,5]])
print("Matrix A is:\northward",A)
impress("Matrix A is:\n",B)
C = np.dot(A,B)
impress("Matrix multiplication of matrix A and B is:\n",C)

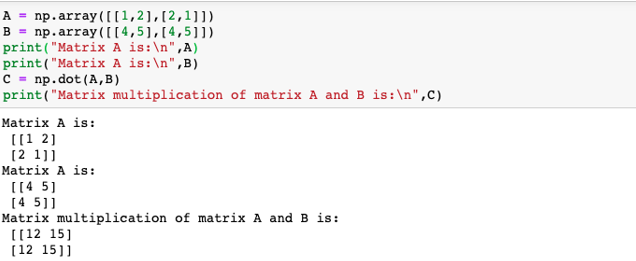
The dot production of given 2D or north-D arrays is calculated in the following ways:

A.B =

ane*four + 2*4 = 12	ane*5+2*5 = fifteen
2*4+ 1*4 = 12	2*5+ 1*5 = 15

Case #5

A program to illustrate the dot product of a scalar value and a 2-D matrix

Lawmaking:

A = np.assortment([[1,one],[1,1]])
impress("Matrix A is:\n",A)
C = np.dot(2,A)
print("Matrix multiplication of matrix A and B is:\n",C)

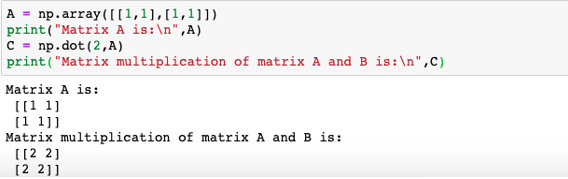
Scalar value = 2

Then, np.dot(2,A) = 2* A

2*A =

1*2 = two	1*ii = 2
1*2 = 2	1*2 = 2

Conclusion

Numpy offers a wide range of functions for performing matrix multiplication. If yous wish to perform element-wise matrix multiplication, so use np.multiply() function. The dimensions of the input matrices should exist the same. And if you have to compute matrix product of two given arrays/matrices and so utilize np.matmul() function. The dimensions of the input arrays should be in the form, mxn, and nxp. Finally, if you have to multiply a scalar value and northward-dimensional array, then utilize np.dot(). np.dot() is a specialisation of np.matmul() and np.multiply() functions.

Recommended Manufactures

This is a guide to Matrix Multiplication in NumPy. Here we discuss the different Types of Matrix Multiplication along with the examples and outputs. You can as well get through our other related articles to learn more–

1. Matrix Multiplication in Java
2. Multidimensional Array in Java
3. NumPy floor()
4. Matrix Multiplication in C++

joskecriew1965.blogspot.com

Source: https://www.educba.com/matrix-multiplication-in-numpy/

Share this post